一、算数运算符的魔法方法
- python2.2以后,对类和类型进行了统一,做法就是讲int()、float()、str()、list()、tuple()这些BIF转换为工厂函数(类对象)
- 给出以下算数运算符对应的魔法方法,前面和后面都被双下划线包尾说明是魔法方法
| 运算符 | 对应的魔法方法 | 中文注释 |
| + | __ add__(self, other) | 加法 |
| - | __ sub__(self, other) | 减法 |
| * | __ mul__(self, other) | 乘法 |
| / | __ truediv__(self, other) | 真除法 |
| // | __ floordiv__(self, other) | 整数除法 |
| % | __ mod__(self, other) | 取余除法 |
| divmod(a, b) | __ divmod__(self, other) | 把除数和余数运算结果结合,divmod(a,b)返回值是一个元组(a//b, a%b) |
| ** | __ pow__(self, other[,modulo]) | self的other次方再对modulo取余 |
| << | __ lshift__(self, other) | 按位左移 |
| >> | __ rshift__(self, other) | 按位右移 |
| & | __ and__(self, other) | 按位与操作 |
| ^ | __ xor__(self, other) | 按位异或操作(同为0,异为1) |
| 丨 | __ or__(self, other) | 按位或操作(有1则1) |
| – | – | – |
- eg:
>>> type(len)
<class 'builtin_function_or_method'> #普通的BIF
>>> type(int)
<class 'type'> #工厂函数(类对象),当调用它们的时候,其实就是创建了一个相应的实例对象
>>> type(dir)
<class 'builtin_function_or_method'>
>>> type(list)
<class 'type'>
>>> a = int('123') #创建一个相应的实例对象a
>>> b = int('345')
>>> a + b #python在两个对象进行相加操作
468
- eg:举个例子,下面定义一个比较特立独行的类:
继承int,并重写__add__方法
>>> class New_int(int):
def __add__(self,other):
return int.__sub__(self,other)
def __sub__(self,other):
return int.__add__(self,other)
>>> a = New_int(3)
>>> b = New_int(5)
>>> a + b #两个对象相加,触发 __add__(self,other)方法
-2
>>> a - b
8
>>>
实例2:错误写法,会造成无限递归
>>> class New_int(int):
def __add__(self,other):
return (self + other)
def __sub__(self,other):
return (self - other)
>>> class New_int(int):
def __add__(self,other):
return (int(self) + int(other)) #将self与other强制转换为整型,所以不会出现两个对象相加触发__add__()方法
def __sub__(self,other):
return (int(self) - int(other))
>>> a = New_int(3)
>>> b = New_int(5)
>>> a + b
8
二、反运算相关的魔法方法
- 反运算相关的魔法方法
| 魔法方法 | 定义 |
| __ radd__(self, other) | 定义加法的行为:+(当左操作数不支持相应的操作时被调用) |
| __ rsub__(self, other) | 定义减法的行为:-(当左操作数不支持相应的操作时被调用) |
| __ rmul__(self, other) | 定义乘法的行为:*(当左操作数不支持相应的操作时被调用) |
| __ rtruediv__(self, other) | 定义真除法的行为:/(当左操作数不支持相应的操作时被调用) |
| __ rfloordiv__(self, other) | 定义整数除法的行为://(当左操作数不支持相应的操作时被调用) |
| __ rmod__(self, other) | 定义取模算法的行为:%(当左操作数不支持相应的操作时被调用) |
| __ rdivmod__(self, other) | 定义当被divmod()调用时的行为(当左操作数不支持相应的操作时被调用) |
| __ rpow__(self, other) | 定义当被power()调用或**运算时的行为(当左操作数不支持相应的操作时被调用) |
| __ rlshift__(self, other) | 定义按位左移位的行为:<<(当左操作数不支持相应的操作时被调用) |
| __ rrshift__(self, other) | 定义按位右移位的行为:>>(当左操作数不支持相应的操作时被调用) |
| __ rand__(self, other) | 定义按位与操作的行为:&(当左操作数不支持相应的操作时被调用) |
| __ rxor__(self, other) | 定义按位异或操作的行为:^(当左操作数不支持相应的操作时被调用) |
| __ ror__(self, other) | 定义按位或操作的行为:丨(当左操作数不支持相应的操作时被调用) |
| – | – |
>>> class int(int):
def __add__(self,other):
return int.__sub__(self,other)
>>> a = int(3)
>>> b = int(2)
>>> a + b
1
反运算与算术运算符的不同之处是,反运算多了一个'r',例如 __add__()的反运算对应为 __radd__()
>>> a + b
这里a是加数,b是被加数,如果a对象的__add__()方法没有实现或者不支持相应的操作,那么python就会自动调用b的__radd__()方法
实例:
>>> class Nint(int):
def __radd__(self,other):
return int.__sub__(self,other)
>>> a = Nint(5)
>>> b = Nint(3)
>>> a + b #由于a对象默认有__add__()方法,所以b的__radd__()没有执行
8
实例2:
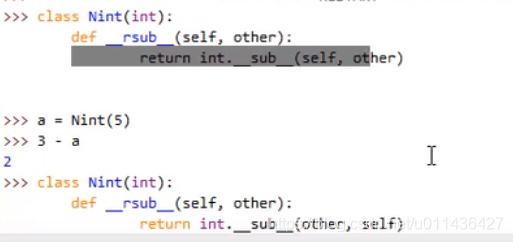
>>> class Nint(int):
def __radd__(self,other):
return int.__sub__(self,other)
>>> b = Nint(5)
>>> 3 + b #由于3无__add__()方法,所以执行b的反运算__radd__(self,other)方法,其中self是b对象
2
eg:注:在重写反运算魔法方法时,一定要注意顺序问题。得到的应该是个负数,所以顺序改变下。
三、增量赋值运算
增量赋值运算的魔法方法
| 魔法方法 | 定义 |
| __ iadd__(self, other) | 定义赋值加法的行为:+= |
| __ isub__(self, other) | 定义赋值减法的行为:-= |
| __ imul__(self, other) | 定义赋值乘法的行为:*= |
| __ itruediv__(self, other) | 定义赋值真除法的行为:/= |
| __ ifloordiv__(self, other) | 定义赋值整数除法的行为://= |
| __ imod__(self, other) | 定义赋值取模算法的行为:%= |
| __ ipow__(self, other) | 定义赋值幂运算的行为:**= |
| __ ilshift__(self, other) | 定义赋值按位左移位的行为:<<= |
| __ irshift__(self, other) | 定义赋值按位右移位的行为:>>= |
| __ iand__(self, other) | 定义赋值按位与操作的行为:&= |
| __ ixor__(self, other) | 定义赋值按位异或操作的行为:^= |
| __ ior__(self, other) | 定义赋值按位或操作的行为:丨= |
| - | - |
四、一元操作符
- 一元操作符的魔法方法
| 魔法方法 | 定义 |
| __ neg__(self) | 定义正号的行为:+x |
| __ pos__(self) | 定义负号的行为:-x |
| __ abs__(self) | 定义当被abs()调用时的行为 |
| __ invert__(self) | 定义按位求反的行为:~x |
| – | – |
到此这篇关于总结Python常用的魔法方法的文章就介绍到这了,更多相关Python魔法方法内容请搜索以前的文章或继续浏览下面的相关文章希望大家以后多多支持!



